Цель: эта статья дает введение в векторы, векторные операции и их приложения в области науки о данных.

Почему вы должны это изучить: это основа почти для всех методов машинного обучения, позволяющих учиться на данных, будь то прогнозирование, классификация или кластеризация.

Оглавление:

• Что такое вектор?
• Сложение вектора
• Умножение скалярных векторов
• Скалярное произведение
• Линейные комбинации

Что такое вектор?

Вектор - это упорядоченный конечный список чисел. Чаще всего их пишут так:

Элементы вектора - это значения в этом векторе. Эквивалентом Python являются массивы numpy. Размер (или длина) вектора - это количество его элементов:

Примеры:

• Вектор объектов: во многих приложениях вектор собирает различные свойства одного объекта. Эти характеристики могут быть измерениями объекта, например, возраста, роста, веса, кровяного давления пациента в больнице.
• Временной ряд: вектор может представлять временной ряд или сигнал, то есть значение некоторой величины в разное время. Например, временные ряды могут представлять стоимость акции на фондовом рынке, а также что-то вроде почасовых осадков в определенном регионе.
• Покупки клиентов: вектор также может представлять собой запись о покупке конкретного клиента у компании, причем записи вектора представляют сумму долларов, потраченных клиентом на определенный продукт.

Сложение вектора

Векторное сложение работает путем поэлементного сложения:

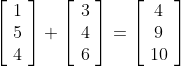
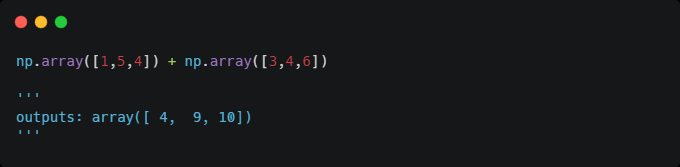
И аналогичным образом векторное вычитание работает поэлементным вычитанием:

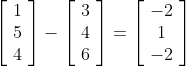
Примеры:

• Количество слов: Если векторы a и b являются количеством слов, обозначающими частоту данного слова в двух соответствующих документах A и B, то сумма a + b дает комбинацию двух документов. Аналогично, разница a-b показывает, сколько раз каждое слово появлялось больше в документе A чем B.
• Временные ряды: если a и b представляют собой временные ряды одного и того же количества, например, ежемесячную прибыль двух магазинов, тогда сумма a + b представляет собой временной ряд общей ежемесячной прибыли двух магазинов.
• Портфель активов: предположим, у нас есть два вектора. Во-первых, исходный вектор портфеля s с записями, обозначающими количество акций данного актива в портфеле. Во-вторых, торговый вектор b с положительными записями, указывающими количество купленных активов, и отрицательными записями - количеством проданных активов. Тогда наш окончательный портфель представлен s + b.

Умножение скалярных векторов

Другой важной векторной операцией является умножение вектора на скаляр (что является просто причудливым словом для «числа»), которое выполняется путем умножения каждого элемента вектора на скаляр:

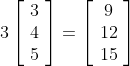
Примеры:

• Требования к материалам: предположим, что вектор q - это спецификация материалов для производства одной единицы некоторого продукта, например мобильного телефона. Тогда записи q - это количество сырья, необходимого для производства одного мобильного телефона. Для производства 300 единиц мобильного телефона требуется сырье на 300 куб .
• Масштабирование звука: если вектор v представляет звуковой сигнал (который, как мы узнали, является временным рядом), громкость сигнала можно увеличить в 3 раза, если мы возьмем скаляр кратный 3v.

Скалярное произведение

Теперь это одна из самых важных операций в линейной алгебре, которая появилась во всех областях, связанных с наукой о данных, от линейной регрессии до нейронных сетей. Скалярное произведение двух векторов вычисляется путем умножения всех соответствующих элементов векторов и сложения полученных произведений.

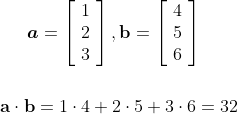
Примеры:

• Сумма: если мы возьмем скалярное произведение векторов a и b, где а состоит только из единиц и имеет ту же длину, что и b, мы получаем операцию суммирования.
• Среднее: если мы возьмем скалярное произведение векторов a и b, где a состоит только из 1/n элементов (n = общая длина векторов), мы получим среднее значение вектора b.
• Сочетание: предположим, что векторы a и b являются векторами одинаковой длины, где элементы могут быть только 0 или 1, тогда скалярное произведение a и b дает общее количество записей, где оба вектора представлены 1. Это может означать в некоторых случаях у нас есть один и тот же прогноз или функция.
• Анализ тональности текста. Специфической проблемой анализа текста является вопрос о том, является ли сантимент (эмоциональная полярность) данного текста положительным, отрицательным или нейтральным. Мы можем использовать начальный подход к этой проблеме, создав два вектора. Во-первых, вектор x длины n, представляющий частоту n слов в тексте. Во-вторых, вектор w одинаковой длины, представляющий полярность данного слова, с записями -1 (для отрицательных слов, таких как «плохо» или «ужасно»), 0 (для нейтральных слов, таких как «и») или 1 (для положительных слов, таких как "приятно" или "потрясающе"). Тогда скалярное произведение x и w дает нам первую (грубую) меру настроения в тексте.

Линейные комбинации

Специальная интерпретация скалярного произведения, когда мы умножаем вектор x на другой вектор β, называется линейной комбинацией x:

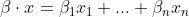
Здесь элементы β называются коэффициентами. Линейные комбинации x составляют основу одного из самых популярных статистических инструментов для прогнозирования непрерывных величин - линейной регрессии. Он используется, например, при прогнозировании цен на жилье, где у нас есть вектор признаков x и мы хотим найти оптимальное взвешивание этих характеристик с помощью коэффициентов регрессии β для прогнозирования цены дома с учетом его характеристик (например, площадь дома в квадратных футах, количество спальных комнат и т. д.)