Распределение вероятностей, которое вы должны знать как специалист по данным

Специалисты по анализу данных сталкиваются с множеством терминов, связанных с вероятностью, при решении задач в интервью и чтении научных статей. Следовательно, знание основ вероятности и распределения вероятностей является обязательным для начинающего специалиста по данным или даже для опытного специалиста. Эти знания помогут вам пройти собеседование, лучше понять данные и разработать более интуитивно понятные решения. В блоге будут следующие разделы.
- Основы вероятности
- Случайная переменная
- Распределения вероятностей и их характеристика
- Равномерное распределение
- Биномиальное распределение
- Гауссово распределение
- Распределение Пуассона
- Экспоненциальное распределение
Не волнуйся. Список огромен, но я постарался сделать этот блог удобочитаемым и понятным. Без лишних слов, давайте углубимся в понимание всех концепций.
Основы вероятности
Предположим, что вероятность того, что событие произойдет, измеряется отношением благоприятных исходов к общим исходам, учитывая, что все исходы одинаково вероятны.
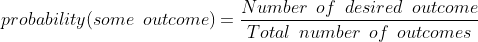
Итак, при подбрасывании монеты
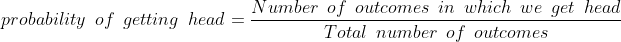
вероятность получить орел = 1/2, если принять во внимание бесконечные испытания.
Случайная переменная
Случайная переменная (RV) - это функция, которая присваивает значения каждому результату эксперимента. Например, при подбрасывании монеты мы определяем случайную величину X как событие, когда появляется орел, а затем давайте посмотрим, как это становится функцией.
Когда результат - орел, X = 1
Когда результат - решка, X = 0
Итак, p (X = 1) = вероятность получить орел = 1/2.
и p (X = 0) = вероятность получить решку = 1/2
Чтобы лучше это понять, давайте рассмотрим еще один пример подбрасывания трех монет. Пусть случайная величина X будет количеством выпавших на трех монетах орлов.
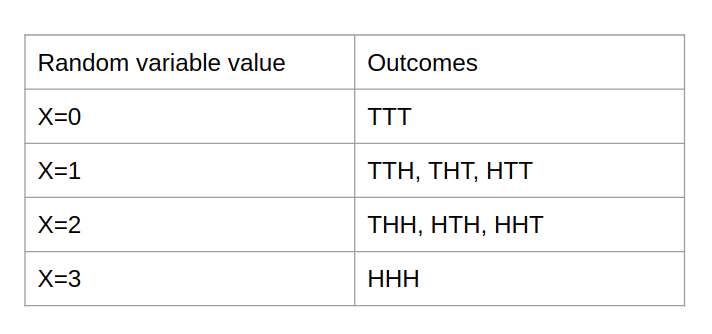
p (X = 1) = вероятность получить хотя бы одного орла = 3/8
Распределение вероятностей и их характеристика
Распределения вероятностей - это совокупность точек данных, описывающих вероятность возникновения события. Распределение вероятностей может быть дискретным или непрерывным. Дискретное распределение - это такое распределение, при котором данные могут принимать только определенные значения, в то время как непрерывное распределение - это такое распределение, при котором данные могут принимать любое значение в пределах указанного диапазона (который может быть бесконечным). Этот набор данных можно визуализировать графически, как показано ниже.
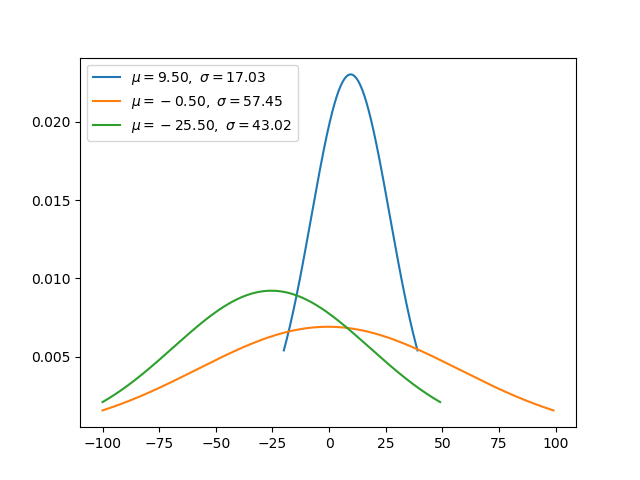
Хорошо, теперь я понимаю, что такое распределение вероятностей. Но насколько это актуально для науки о данных? В науке о данных мы часто формируем суждения о параметрах совокупности и надежности статистических отношений на основе случайной выборки данных. В таких случаях распределения вероятностей помогают нам делать эти суждения.
Каждое распределение данных имеет разные формы на графике. Таким образом, должна быть какая-то метрика, которая могла бы помочь нам понять форму распределения без фактического нанесения данных на график. Метрики, которые могут предоставить информацию о распределении: среднее, дисперсия и стандартное отклонение. Давайте разберемся с каждым из них.
Среднее значение
Это среднее значение точек данных и обозначается μ. Например, если у нас есть дискретный набор данных как {1,2,3,4,5}, тогда среднее значение (μ) будет 3 ((1 + 2 + 3 + 4 + 5) ÷ 5). Он используется для нахождения числа, при вычитании которого из всех точек данных среднее значение преобразованных данных будет равно нулю.
Дисперсия
Дисперсия - это среднее значение квадрата разницы между точкой данных и средним значением. Обозначается он σ². В приведенном выше примере дисперсия (σ²) будет 2,5 ((1–3) ² + (2–3) ² + (3–3) ² + (4–3) ² + (5–3) ²) ÷ 5).
Стандартное отклонение
Это квадратный корень из дисперсии, обозначаемый σ. В приведенном выше примере стандартное отклонение (σ) будет 1,58 (\ sqrt {2.5}). Он используется для измерения разброса чисел в наборе данных. Небольшое стандартное отклонение означает, что точки данных расположены ближе друг к другу.
Равномерное распределение
Мы поняли, что такое вероятностное распределение и каковы его характеристики. Давайте теперь разберемся с равномерным распределением вероятностей. Равномерное распределение - это простейшее распределение вероятностей, которое также известно как прямоугольное распределение. Это распределение имеет постоянную вероятность. Наиболее распространенным примером этого типа раздачи может быть подбрасывание монеты или кости.
Для дискретного распределения вероятностей
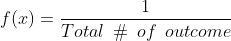
Для непрерывного
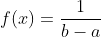
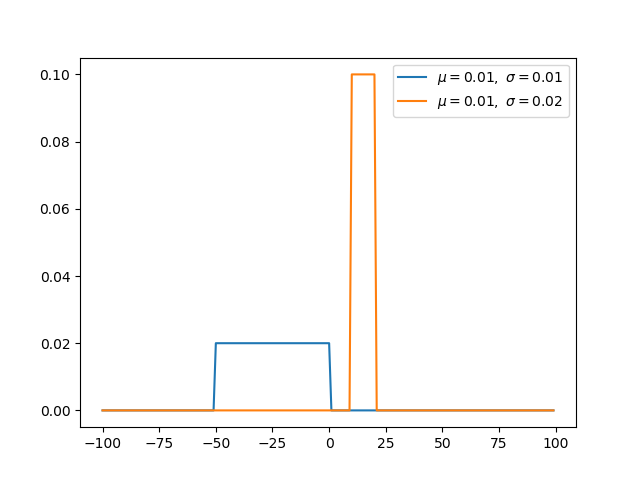
Равномерное распределение используется для метода начальной загрузки для расчета доверительных интервалов. Кроме того, моделирование методом Монте-Карло начинается с генерации равномерно распределенных псевдослучайных чисел.
Биномиальное распределение
В биномиальном распределении случайная величина определяется как количество успехов в n независимых повторных испытаниях. Пусть вероятность успеха равна p, поэтому формула для биномиального распределения вероятностей имеет вид
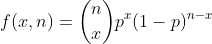
Пример: если вы покупаете лотерейный билет, вы либо выигрываете деньги, либо нет. Любое событие, о котором вы можете подумать, которое имеет два возможных исхода, может быть представлено биномиальным распределением. В науке о данных биномиальное распределение полезно для анализа статистики задач двоичной классификации.
Гауссово / нормальное распределение
Это одно из самых известных распределений, и многие явления реального мира, такие как ошибка измерения, рост людей, оценки людей в тесте и т. д., следуют этому распределению. Формула этого распределения выглядит следующим образом:
Как обсуждалось выше, μ - это среднее значение, а σ - стандартное отклонение.
Обратите внимание, что это распределение имеет колоколообразную структуру, и пик колокола соответствует среднему значению, тогда как стандартное отклонение связано с шириной колокола.
Нормальное распределение становится стандартным нормальным распределением, когда среднее значение равно 0, а стандартное отклонение равно 1.
Этот дистрибутив имеет широкое применение в жизни специалиста по данным, и его необходимо знать. Существует множество моделей машинного обучения, таких как регрессия на основе наименьших квадратов, Гауссовский наивный байесовский классификатор, линейный и квадратичный дискриминантный анализ и т. д., предназначенных для работы с наборами данных, которые следуют нормальному распределению.
Распределение Пуассона
Распределение Пуассона часто называют распределением редких событий. Если у вас есть событие, которое происходит с фиксированной скоростью, например, 5 человек заходят на стадион каждую секунду или 2 манго созревают каждую минуту на ферме. Тогда вероятность наблюдения n событий в единицу времени может быть рассчитана с использованием распределения Пуассона, используя приведенную ниже формулу.
где μ - частота событий в единицу времени.
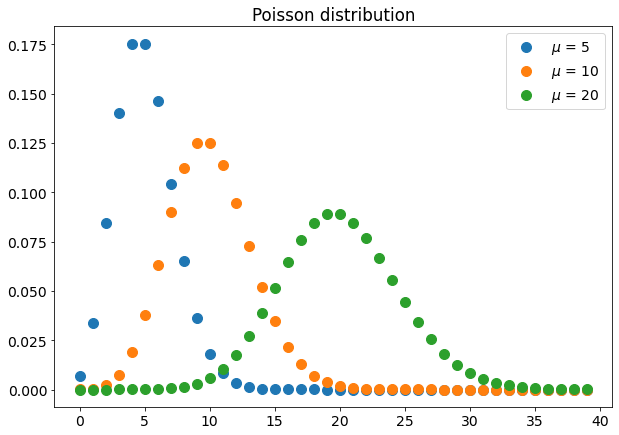
Многие реальные явления, такие как автомобильные аварии, транспортный поток, генетические мутации и количество опечаток на странице, следуют распределению Пуассона. Многие владельцы магазинов используют распределение Пуассона для прогнозирования количества покупателей, которые придут в их магазин.
Экспоненциальное распределение
Экспоненциальное распределение тесно связано с распределением Пуассона. Если событие Пуассона происходит в фиксированный интервал времени, интервал времени между двумя последовательными событиями Пуассона распределяется экспоненциально. Вероятность наличия временного интервала t между двумя последовательными пуассоновскими событиями следующая:
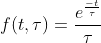
где t - средний временной интервал между двумя последовательными Пуассоновскими событиями.
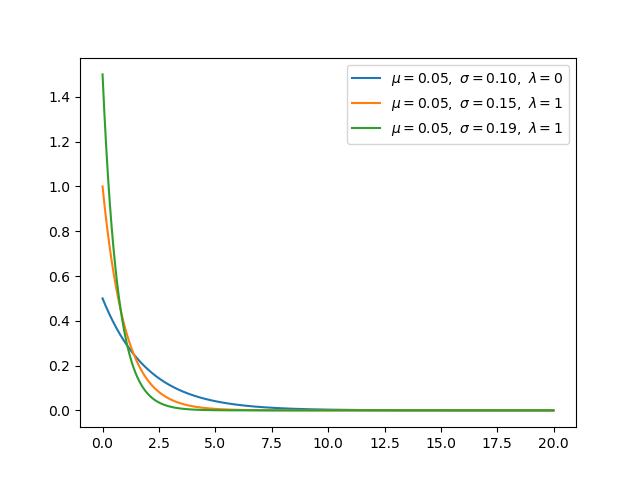
Экспоненциальное распределение имеет ограниченное использование в науке о данных. В общем, если вы хотите перейти от Пуассоновского процесса (в котором вы изучаете количество событий) к временной области, то экспоненциальное распределение является наиболее подходящим распределением.
Заключение
Итак, мы обсудили 5 различных распределений вероятностей и рассмотрели варианты использования каждого распределения в жизни специалиста по данным. Я надеюсь, что вам понравилась эта статья, и я всегда буду рад услышать ваши отзывы об улучшении читабельности блога.